사원수, 쿼터니언 (Quaternion)

---

행렬을 쓰지 않는 이유

복소수에 대해

복소수에서 곱하기의 기하학적 의미

3차원 복소공간을 가지는 복소수?

사원수에서의 회전

공식유도

사원수 (Quaternion) 회전의 장점

---

이전 글 : Unity에서의 짐벌 락

Unity에서 짐벌 락 (Gimbal Lock) 관찰하기

오일러 각오일러 각의 문제오일러 각의 표현짐벌 락 (Gimbal Lock) 문제순서에 따라 결과가 바뀌는 문제 사원수(Quaternion)를 쓰는 이유에 대해 너무나도 궁금했는데, 이번 기회에 알게되어 정리해본다. 오일러 각 Inspector를 보면 Transform에서 볼 수 있는 Rotation을 보면 3차원의 정보로 표현이 되어 있다. 사실 너무 직관적이고 당연해보인다.3차원 물체니까 3차원의 정보를 표현한다는 것이니깐… X값을 변화하면 빨간색을 중심으로 회전한다. Y값을 변화하면 초록색을 중심으로 회전한다. Z값을 변화하면 파란색을 중심으로 회전한다. 오일러 각의 문제 항상 그대로만 동작하면 문제가 없겠지만, 조금만 값을 바꿔보면 이상한 점을 발견할 수 있다. Rotation이 X = 90, Z ..

https://seoksii.tistory.com/45

지난 시간에 짐벌락에 대해 다뤘었다.

유니티에서는 회전을 계산할 때 오일러 각이 아닌 사원수 (Quaternion) 를 사용하게 된다.

사원수를 왜 쓰는지, 그리고 이것으로 물체의 회전을 어떻게 계산하는지 알아보고자 한다.

---

행렬을 쓰지 않는 이유

행렬로도 회전변환이 가능하다.

위키피디아에서 보면 $\vec{u}=(x,y,z)$를 축으로 반시계 방향으로 $\theta$만큼 회전하는 행렬은 다음과 같다.

$$R=\begin{bmatrix} cos\theta+x^2(1-cos\theta)&xy(1-cos\theta)-zsin\theta&xz(1-cos\theta)+ysin\theta \\ yx(1-cos\theta)+zsin\theta & cos\theta+y^2(1-cos\theta)&yz(1-cos\theta)-xsin\theta \\ zx(1-cos\theta)-ysin\theta & zy(1-cos\theta)+xsin\theta & cos\theta+z^2(1-cos\theta) \end{bmatrix}$$

그러나 회전 행렬 변환은 다음과 같은 문제를 가지고 있다.

• 점유 메모리 영역이 너무 크고 계산 부하가 높다.

• 계산 과정에서 많은 오차가 발생한다.

• 매끄러운 회전을 위한 보간(Lerp)을 표현하기가 힘들다.

따라서 유니티에서는 사원수(Quaternion)을 사용하고 있다.

---

복소수에 대해

$$z = x + iy$$

고등학교 때 한 번쯤은 배우게 되는 복소수.

왜 복소수 이야기가 갑자기 나오냐면, 사원수는 복소수의 확장으로 정의되는 수 체계이기 때문이다.

일단, 가장 먼저 짚고 넘어가야 하는 것.

복소수는 벡터이다.

복소평면 상에서 나타내어지는 벡터라는 것이다.

$$z=x+iy=(Re(z),Img(z))=(x,y)$$

복소수에서 곱하기의 기하학적 의미

복소수를 배울 때, $i^2=-1$ 이라는 것 하나로, i의 거듭제곱을 계산하는 문제가 자주 나왔다.

$$1\overset{\times i}{\longrightarrow} i\overset{\times i}{\longrightarrow} -1\overset{\times i}{\longrightarrow} -i\overset{\times i}{\longrightarrow} 1$$

이 i를 곱한다는 것.

기하학적으로는 복소평면 상에서의 90도 회전을 의미한다.

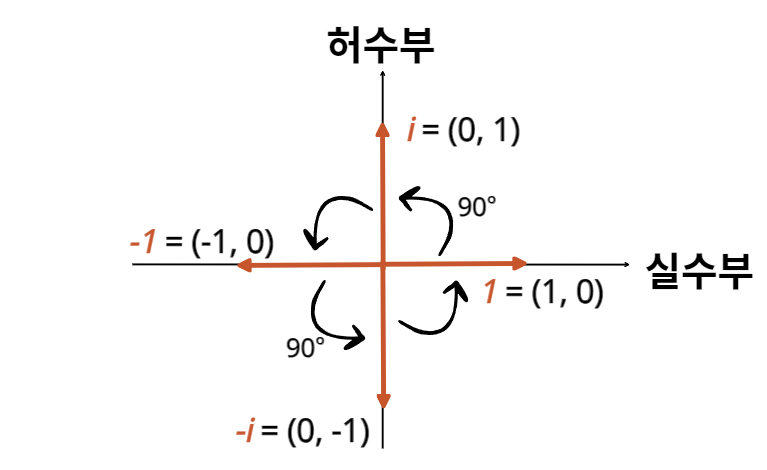
즉, 정리하자면 이렇다.

실수의 곱셈은 복소평면 벡터의 크기를 변화시키고, (Scaling) 허수의 곱셈은 복소평면 벡터를 회전시킨다! (Rotation)

90도가 아닌 다른 형식 역시 복소수의 곱셈만으로 나타낼수 있고, 오일러 형 (Euler’s Form)으로 더욱 쉽게 나타낼 수 있다.

$$r(cos\theta + isin\theta) = e^{i\theta}$$

잘 감이 오지 않는다면, 유튜브의 다음의 재생목록을 참고하자.

Imaginary Numbers Are Real [Part 1: Introduction]

For early access to new videos and other perks: https://www.patreon.com/welchlabs Want to learn more or teach this series? Check out the Imaginary Numbers are Real Workbook: http://www.welchlabs.com/resources. Imaginary numbers are not some wild invention, they are the deep and natural result of extending our number system. Imaginary numbers are all about the discovery of numbers existing not in one dimension along the number line, but in full two dimensional space. Accepting this not only gives us more rich and complete mathematics, but also unlocks a ridiculous amount of very real, very tangible problems in science and engineering. Part 1: Introduction Part 2: A Little History Part 3: Cardan's Problem Part 4: Bombelli's Solution Part 5: Numbers are Two Dimensional Part 6: The Complex Plane Part 7: Complex Multiplication Part 8: Math Wizardry Part 9: Closure Part 10: Complex Functions Part 11: Wandering in Four Dimensions Part 12: Riemann's Solution Part 13: Riemann Surfaces Want to learn more or teach this series? Check out the Imaginary Numbers are Real Workbook: http://www.welchlabs.com/resources.

https://www.youtube.com/watch?v=T647CGsuOVU&list=PLiaHhY2iBX9g6KIvZ_703G3KJXapKkNaF

필자는 푸리에 변환을 배울 때 너무나도 큰 도움이 되었던 영상이다.

---

3차원 복소공간을 가지는 복소수?

처음에는 이렇게 생각할 수 있다.

허수부를 한 개 더 추가한, 일종의 삼원수를 사용하면 될 것 같은데?

아쉽지만 아니다.

애초에 삼원수는 존재하지 않는다.

실수부 한개, 허수부 두개가 존재한다고 가정하고 곱셈을 통해 회전을 시켜보면, 허수부 둘 중 하나는 실수라는 모순이 나오기 때문이다.

우리는 저번 게시글에서 3차원 공간의 회전 데이터를 한 번에 표현하려면, 4차원의 정보가 필요하다는 것을 알았다.

즉, 실수부 1개 + 허수부 3개를 가진 4차원 공간은 가능한가?라는 질문이 자연스레 이어지고, 그 답은 이번 글에서 다루고 있는 사원수가 되겠다.

---

사원수에서의 회전

사원수는 다음과 같이 표현한다.

$$Q = a+bi+cj+dk=(a,i,j,k)=(a,V)$$

위 공식에서 벡터 $V$는 허수부 $(i,j,k)$를 한 번에 벡터로 나타낸 것이다.

그래서 사원수를 이야기할 때 실수부 $a$를 스칼라부, 허수부 $V$를 벡터부라고 부르기도 한다.

사원수의 작동방식은 다음과 같은 방정식에서 시작한다.

$$i^2=j^2=k^2=ijk=-1$$

아까 복소수처럼 곱셈을 기하적으로 표현해보자.

첫번째로, $i$를 곱하는 것은 $i$ 축을 중심으로 회전을 하겠다는 소리이다.

$Q=j$일 때 즉, $(0, (0,1,0))$일 때 $i$를 계속해서 곱해주면 다음과 같다.

$$j\overset{\times i}{\longrightarrow} k\overset{\times i}{\longrightarrow} -i\overset{\times i}{\longrightarrow} 1\overset{\times i}{\longrightarrow} i\overset{\times i}{\longrightarrow} -1\overset{\times i}{\longrightarrow} -i\overset{\times i}{\longrightarrow} ...$$

???

복소수일 때랑은 살짝 다르다.

복소수에서는 곱셈 그 자체가 회전이지만, 사원수는 말그대로 회전을 나타내는 것은 아니고, 사원수로 3차원 공간에서의 회전을 나타내기 위해 여러 가지 제약조건을 걸어서 연산에 활용하게 된다.

어떻게 활용하냐면, 3차원의 회전을 사원수로 계산할 때는 사원수의 허수부만 이용한다.

즉, 3차원의 오일러각을 담은 벡터를 사원수로 변환할 때 허수부의 벡터로 변환한다는 말이다.

이 때 회전변환을 하는 사원수를 $q$라고 하면, 단순히 $q$를 곱해주는 것은 벡터를 회전시킨다고 볼 수 없다.

$q$를 곱해주는 순간 3차원 공간 상에 있던 벡터가 사원수의 4차원 복소공간으로 넘어가버린다!

엄밀히 말하자면, 우리는 3차원의 벡터를 실수부가 0인 사원수로 변환했기에, 이를 4차원 복소공간에서 관찰하면 스칼라부 = 0인 3차원 투영공간에 존재하는 벡터로 볼 수 있는 것이다.

우리가 얻고자 하는 값은 역시 회전 변환이 이루어진 벡터.

즉, 결과값도 스칼라부 = 0인 3차원 투영공간에 존재해야 한다!

그러려면 어떻게 해야하는가?

간단하다.

한 번의 사원수 곱셈으로 스칼라부 ≠ 0인 복소공간으로 튀어나와버린 벡터를 스칼라부 = 0인 공간으로 다시 집어넣는 작업을 해주면 되는 것이다.

곱셈이 두 번 필요하다!라고 이해하면 되는 것이다.

공식유도를 살짝 해보자.

공식유도

참고로 사원수의 곱셈을 (스칼라부, 벡터부)로 표현했을 때는 다음과 같이 표현할 수 있다.

$$q_1 \times q_2 = (s_1,\vec{v_1}) \times (s_2,\vec{v_2}) =(s_1s_2- \vec{v_1} \cdot \vec{v_2},\ s_1\vec{v_2}+s_2\vec{v_1} + \vec{v_1}\times\vec{v_2})$$

이 때 3차원 벡터를 사원수로 나타낸 값 $p=(0,\vec{v})$에 대해 회전변환을 마친 벡터 $p'=(0,\vec{v}')$을 구하기 위해

사원수 $q_1=(\alpha_1+\beta_1\vec{w_1})$와 $q_2=(\alpha_2+\beta_2\vec{w_2})$를 각각 곱해준다고 해보자.

이 때 $\vec{v},\ \vec{w_1},\ \vec{w_2}$는 길이가 1인 단위벡터이다.

$$p'=q_1 v q_2= (\alpha_1+\beta_1\vec{w_1})\times (0,\vec{v})\times (\alpha_2+\beta_2\vec{w_2})\\ = (-\beta\vec{v}\cdot\vec{w_1},\ \alpha_1\vec{v}+\beta_1\vec{w_1}\times\vec{v})\times (\alpha_2+\beta_2\vec{w_2})\\ =(-\alpha_2\beta_1\vec{v}\cdot\vec{w_1}-\alpha_1\beta_2\vec{v}\cdot\vec{w_2}-\beta_1\beta_2(\vec{w_1}\times\vec{v})\cdot\vec{w_2},\\ -\beta_1\beta_2(\vec{v}\cdot\vec{w_1})\vec{w_2}+\alpha_1\alpha_2\vec{v}+\alpha_2\beta_1\vec{w_1}\times\vec{v}+\alpha_1\beta_2\vec{v}\times\vec{w_2}+\beta_1\beta_2\vec{w_1}\times\vec{v}\times\vec{w_2})$$

즉, 위 공식대로면 실수부 $-\alpha_2\beta_1\vec{v}\cdot\vec{w_1}-\alpha_1\beta_2\vec{v}\cdot\vec{w_2}-\beta_1\beta_2(\vec{w_1}\times\vec{v})\cdot\vec{w_2}=0$이기만 하면 된다.

이 때 $\alpha_1=\alpha_2,\ \beta_1=\beta_2,\ \vec{w_1}=-\vec{w_2}$라는 constraints를 추가해주면, 실수부가 0이 된다!

해당 constraints는 $q_1$과 $q_2$를 켤레 관계로 만드는 제약 조건이다.

$$q_1=\overline{q_2}\\$$

이 때 $\alpha=\alpha_1=\alpha_2,\ \beta=\beta_1=\beta_2,\ \vec{w_1}=-\vec{w_2}$로 놓고 벡터부를 계산하자.

$$-\beta_1\beta_2(\vec{v}\cdot\vec{w_1})\vec{w_2}+\alpha_1\alpha_2\vec{v}+\alpha_2\beta_1\vec{w_1}\times\vec{v}+\alpha_1\beta_2\vec{v}\times\vec{w_2}+\beta_1\beta_2\vec{w_1}\times\vec{v}\times\vec{w_2}\\ =\beta^2(\vec{v}\cdot\vec{w_1})\vec{w_1}+\alpha^2\vec{v}+2\alpha\beta\vec{w_1}\times\vec{v}-\beta^2\vec{w_1}\times\vec{v}\times\vec{w_1} \\ =\beta^2(\vec{v}\cdot\vec{w_1})\vec{w_1}+\alpha^2\vec{v}+2\alpha\beta\vec{w_1}\times\vec{v}+\beta^2(\vec{w_1}\cdot\vec{v})\vec{w_1}-\beta^2(\vec{w_1}\cdot\vec{w_1})\vec{v}\\ =(\alpha^2-\beta^2)\vec{v}+2\alpha\beta\vec{w_1}\times\vec{v}+2\beta^2(\vec{v}\cdot\vec{w_1})\vec{w_1}$$

지금까지의 계산은 다음과 같다.

3차원 벡터를 사원수로 나타낸 값 $p=(0,\vec{v})$와 사원수 $q=(\alpha+\beta\vec{w})$에 대해 (단, $\vec{w}$는 길이가 1인 단위벡터)

$$p'=qp\overline{q}\\=(0,\ (\alpha^2-\beta^2)\vec{v}+2\alpha\beta\vec{w}\times\vec{v}+2\beta^2(\vec{v}\cdot\vec{w})\vec{w})$$

이제 다 왔다.

위에서 정리된 식은, 로드리게스 회전 공식과 똑같은 꼴을 가지고 있다!

Rodrigues' rotation formula

In the theory of three-dimensional rotation, Rodrigues' rotation formula, named after Olinde Rodrigues, is an efficient algorithm for rotating a vector in space, given an axis and angle of rotation. By extension, this can be used to transform all three basis vectors to compute a rotation matrix in SO(3), the group of all rotation matrices, from an axis–angle representation. In terms of Lie theory, the Rodrigues' formula provides an algorithm to compute the exponential map from the Lie algebra so(3) to its Lie group SO(3).

https://en.wikipedia.org/wiki/Rodrigues'_rotation_formula

로드리게스 회전 공식에 의하면 3차원 공간의 벡터 $\vec{v}$를 $\vec{u}=(x,y,z)$를 축으로 반시계 방향으로 $\theta$만큼 회전한 벡터 $\overrightarrow{v_{rot}}$은 다음과 같다.

$$\overrightarrow{v_{rot}}=\vec{v}cos\theta+(\vec{u}\times\vec{v})sin\theta+\vec{u}(\vec{u}\cdot\vec{v})(1-cos\theta)$$

증명과정이 매우 복잡하니 참고만 해두자.

즉, 사원수 곱셈 결과에 따르면 이렇게 쓸 수 있다.

$$\alpha^2-\beta^2=cos\theta\\ 2\alpha\beta=sin\theta\\ 2\beta^2=1-cos\theta$$

위 식을 모두 만족하는 $\alpha$와 $\beta$가 있다면 끝이다.

고등학교 때 삼각함수의 반각공식과 배각공식을 들어보지 않았는가?

그렇다. 위 세 식을 만족하는 값은 $\alpha=cos{\theta\over2},\ \beta=sin{\theta\over2}$ 이다.

이제 결론이다!

로드리게스 회전 공식에 의하여 3차원 공간의 벡터 $\vec{v}$를 사원수로 나타낸 값 $p=(0,\vec{v})$에 대하여 $\vec{u}=(x,y,z)$를 축으로 반시계 방향으로 $\theta$만큼 회전한 벡터 $\vec{v}'$의 사원수 값 $p'=(0,\vec{v}')$는 다음과 같이 구할 수 있다.

$$p'=qp\overline{q} \\ q=(cos{\theta\over2},\ sin{\theta\over2}\ \vec{u})$$

---

사원수 (Quaternion) 회전의 장점

• 짐벌락이 발생하지 않는다.

회전을 세 번에 걸쳐 나누어 계산하는 것이 아니라 임의의 축에 대해 회전을 계산하기 때문에 짐벌락 현상이 아예 없다.

• 계산 자체의 정확도가 높다.

무슨 말인가 싶을텐데, 회전 변환 행렬의 경우 계산과정에 삼각함수가 굉장히 자주 들어간다.

삼각함수 자체도 다른 연산에 비해 무겁지만, 결과가 -1f~1f로 매우 좁기 때문에 부동소수점으로 인한 오차가 계속해서 누적된다!

• 연산이 빠르며 행렬에 비해 메모리를 적게 사용한다.

계산이 이루어질 때, 행렬 곱이 아닌 벡터 연산처럼 이루어지기 때문에 행렬에 비해 훨씬 빠르고, 메모리 공간 역시 적게 차지한다.

• 매끄러운 보간(Lerp) 표현이 가능하다.

90도 회전 변환을 천천히 한다면 이를 1.5도짜리 회전 변환 60번을 하는 사원수로 바꿔 이 사원수를 앞뒤로 계속 곱해주기만 하면 되는 것이다.

행렬의 경우 이것이 힘든 이유가, 매 회전 변환을 할 때마다 행렬이 새로 계산되기 때문이다.

---

지금까지 사원수(Quaternion)를 이용한 회전 연산에 대해 알아봤다.

사실 기본적으로 오일러각을 사원수로 변환한다던지, 보간 등의 기능을 유니티에서 전부 지원하기 때문에 해당 내용을 반드시 숙지하고 있어야할 이유는 없지만,

짐벌락 발생이 우려된다거나, 사원수를 직접 사용할 일이 있을 때 해당 내용에 대해 직관을 가지고 있는 것이 큰 도움이 되리라 생각한다.

Uploaded by N2T